11x11x11 – история одной головоломки
В этой статье речь пойдет о кубиках Рубика больших порядков, в частности об одном из наибольших существующих на сегодня – 11x11x11. Став его счастливым обладателем, как самого сложного пазла, – мне бы хотелось вам описать всю палитру возникающих ощущений, в то время как держишь в руках эту головоломку.
Рубик, кубик, куб, 11*11*11, 11x11x11, головоломка, пазл, ви-куб, большой, сборка, решение, разобранный, тест, обзор,
Rubik, cube, puzzle, twist, toy, v-cube, big, solve, solving, scramble, disassemble, test, review
Главы:
1. Преамбула.
2. История появления.
3. Ожидаемое лучше самого ожидания!
4. Попытка номер “раз”.
5. Напутствие к сборкам 11x11x11.
6. Головоломка в головоломке.
7. Заключение.
Классический кубик Рубика, изобретенный венгром Эрно Рубиком, имеет порядок 3x3x3 – то есть по три маленьких кубика на каждую сторону грани. С развитием технической мысли стало возможным реализовать во плоти кубики большего порядка: 4x4x4 и 5x5x5, с такими же правилами игры, как и в оригинальной головоломке. Их решение, как и следует ожидать, требует несколько большего усердия и навыков. Конечно, в виртуальном пространстве, с помощью компьютерных программ, можно симулировать размеры вплоть до 20x20x20, и более. Но куда значительнее удовольствие получаешь, имея возможность повертеть их в руках. Долгое время считалось невозможным в механике придумать кубики порядком большие, чем 5x5x5. Однако, и таковые появились, с возможностью наращивания слоев вплоть до физического предела устойчивости конструкции. Самый большой куб, который я имею возможность вам презентовать – это 11x11x11. О нем и пойдет речь…
Вы наверняка имеете соображение, откуда пошло слово “головоломка”. Изначально оно имело прямое значение, но в итоге стало использоваться в своем переносном смысле: как задача, требующая решения на сообразительность. Ради сарказма сказать, оговариваемый куб такого громадного порядка может и вправду служить головоломкой в её исконном значении. Этот пазл весит 908 грамм – почти килограммовая махина, и в поперечном размере составляет 11.5 см – так что даже ладонью обхватить трудно.
Мне довелось приобрести куб 11x11x11 по счастливой случайности. До тех пор я долго грезил желанием собирать все сложные и сложные головоломки. Однажды я заказал комплект V-Cube 5, 6 и 7 – это было похоже со стороны на радость ребенка. По сути, этим и является, я не отрицаю :). Но мне жутко хотелось собирать кубы, на решение которых уходили бы не секунды (как в случае с классическим кубиком Рубика), а минуты и даже часы. Спидкубинг (speedcubing) не был моей прерогативой – я стремился постичь математическую суть, сборку на оптимальность, находить и совершенствовать существующие методы сборки одного из самых известных в мире пазлов. Для этого мне нужен был простор, место где развернуться, – и его я находил в кубах больших размерностей, и головоломках подобных кубику: мегаминксе, пирамидке и т.д. Так вот, решение 5x5x5, 6x6x6 и 7x7x7 приносило тянущиеся минуты наслаждения, и расширение границ применения известным алгоритмам сборки.
Все бы хорошо, но и этого со временем оказалось мало. В голове роились мысли и предположения: а как поведет себя тот или иной метод решения в более сложных ситуациях? И, в конце концов, каков может быть применен принцип для общего случая? Наравне с этим, как теоретической частью, – я искал возможность получения реальной головоломки, самой большой и самой сложной. Размер пал на 11x11x11 – как оптимальный: не слишком большой и дорогой, но и кардинально отличающийся от всех прежде имеющихся. Я не сидел на месте, а предпринял попытку самому изготовить столь вожделенный пазл. Не будучи пустословом, привожу ссылку, где я опубликовывал свои труды: ’11x11x11 Куб в стиле Пагоды’

click to zoom to actual resolution
В проектировании я начинал с математических основ, которыми описывал соотношения размеров, движения слоев и поворотов граней. И таким образом вывел оптимальный, на мой взгляд, внешний вид головоломки. Но дело обстояло куда сложнее с ее внутренним механизмом состыковки отдельных деталей. В качестве базиса я позаимствовал ранее никем не использовавшуюся идею Оскара, одного из уважаемый изобретателей пазлов. В итоге, после пары месяцев усердной работы, я получил пригодную модель. Но мне не суждено было её воплотить в жизнь за неимением доступных средств.






click to zoom to actual resolution
Видимо, за мои отчаянные старания, и искреннее желание познания, я был награжден. Не моими руками, но всё же доставшийся мне по воле хорошего знакомого – куб 11x11x11 появился в моей коллекции головоломок. Он облетел в своей тесной посылке более полумира, и приземлился окончательно в аэропорту моего города. Неизбежная волокита с растаможкой, регистрацией, проверкой, доставкой на почтовое отделение, пару телефонных звонков, всё прошло как по маслу – и вот посылка у меня в руках! Радости нету предела: неужели то, о чем я так долго помышлял, но и представить не мог, что оно вовсе существует – сейчас находится в этой картонной коробке?! Не буду тянуть ожидание, весь процесс первого созерцания вы можете увидеть в моем видео, которое я снял напамять:

click to open video
Видео: 11x11x11 Cube unbox (now in Ukraine)
Глава 3. Ожидаемое лучше самого ожидания!
Первое что замечаешь, глядя на кубик 11x11x11 – это его вовсе не кубическая форма. Почему так? Ну, во-первых, такова особенность внутренней конструкции, которая решает проблему крепления угловых элементов. Они нанизаны на стержни, уходящие в сердцевину механизма. Иначе при поворотах внешних граней им не за что будет держаться. Такая мера необходима, уже начиная с кубов порядка 7x7x7. Во-вторых, скругление внешней формы даёт возможность уютнее расположить такой крупный объект на ладони. Бросается в глаза также огромное количество составных элементов, которые кажутся столь малыми, по сравнению с классическим кубиком Рубика. Это само собой разумеющееся, в ином случае общие размеры были бы сопоставимы с баскетбольным мячом. Со временем привыкаешь и не чувствуешь дискомфорта – разглядеть цветные наклейки всё же не трудно.
Заполучив в руки этого исполина – долго вертишь, удивляясь его прочности. Ведь, немного зная особенности его внутреннего строения – диву даешься устойчивости всей конструкции. По сути основа такого дизайна – это расходящиеся во все стороны конусные сечения, вдоль которых проворачиваются слои куба. В таком случае, все составные элементы крепятся друг на дружке, и, как бы, расходятся веером от геометрического центра головоломки. Об этом поподробнее я расскажу далее в статье.
Первые впечатления оказались очень приятными: пластик, из которого сделан кубик, просто замечательный: не крошится и не гнется. Что меня действительно удивило, так это то, что такая громадина крутится прямо из упаковки без какой-либо предварительной балансировки. Обычно же, профессиональные агрегаты требуют подготовки и подгонки перед использованием. Имея удовольствие доселе крутить в руках 7x7x7, как самый большой кубик, – я думал, что уж такую махину, как 11x11x11, пришлось бы полировать и обильно поливать силиконовой смазкой, чтобы добиться приемлемой легкости кручения. Ведь площадь обоюдного соприкасания деталей значительная. Однако, качество литья кубика превзошло все ожидания. Как я позже узнал, после разборки, – никакой смазки внутри даже и не было.
На фоне такого качества пластика, немного разочаровали стикеры (sticker) – цветные наклейки. Не то, чтобы они были криво наклеены или отлетали, – тут претензий нету. Выбранный материал – цвет металлик, отсвечивал бликами, и некоторые цвета сливались. Так вот, оранжевый сильно похож на красный, и это особенно чувствуется на смешанном кубике. Что правда, приятной мелочью в комплекте шёл дополнительный набор наклеек, т.к. достать еще один по износу старых, было бы трудно.
Третий критерий оценки – функциональность кубика. Крепящие винты на сердцевине – очень жесткие, куда жестче, чем у 7x7x7. В общем-то, чего и следовало ожидать, поскольку плече прилагаемой силы, для поворота грани, большее – а потому основной крепящий элемент (центральный на пружине) должен в большей мере противиться усердию его “вывернуть наружу”. В спидкубинге есть такой термин: “резать углы” – он означает способность конструкции головоломки провернуть внешние слои с не до конца выровненными слоями в перпендикулярном направлении. И кто бы мог подумать, что даже на таком большом порядке, как 11x11x11, будет возможность применять этот трюк! Этому в заслугу использованный внутренний дизайн концентрических конусов. Я однажды предрекал столь большим головоломкам основное неудобство при сборке: это выравнивание слоев по завершению очередного поворота. И предлагал решение: использование clicking-механизма, по аналогии с кубом V-Cube 6. Этого, всё же, очень не хватает в 11x11x11.
У кубов больших размерностей существует проблема выпадения отдельных кусочков. Это случается из-за очень быстрого вращения с нечетко выровненными слоями, либо небрежном использовании: если кубику, что называется, “скрутить голову” – то он начнет рассыпаться в руках. К этому стоит привыкнуть: такие сложные головоломки – сложны и внутри, а потому, зачастую, и хрупкие. Особенно это можно ощутить на 7x7x7 – там чаще всего выпадает один и тот же элемент. Причина тому – его неглубокое залегание “корнями” внутри конструкции. Когда я впервые брал в руки 11x11x11 – думал, что эта проблема будет еще актуальней.
Но на практике оказалось два удивительных вывода. Во-первых, потенциально может выпасть элемент, располагающийся абсолютно на том самом месте (а не наиболее приближенный к краю куба, как я считал ранее). Во-вторых, прочность крепления элементов зависит скорее не от глубины залегания, сколько от величины зазоров между кусочками на поверхности кубика. Причем, плотность прилегания может быть сколь угодно высокой – на проворачиваемости слоев куба это практически не отражается (здесь свою роль играет жесткость пружин, на которых всё держится). 11x11x11 в этом плане достаточно прочен, чтобы утверждать: ни разу всё время у меня не было выпадения элементов (pops), либо их “зажевывания” при недопроворотах.

На самом деле, очень долго не решаешься перемешать (scramble), такой большой куб, после того как его впервые получаешь. И дело не в том, что боишься его затем не сложить – алгоритм складывания таких громадин практически уже не отличается после размера 5x5x5. Вопрос во времени: сколько же на это уйдет времени?! Для человека не столь чемпионских амбиций по складыванию кубика Рубика: для решения 3x3x3 – надо в среднем 30 секунд; для 5x5x5 – до 4-х минут; решение 7x7x7 – можно уложить в 11 минут. Так сколько же надо выделить свободного времени для 11x11x11?.. Помнится, как однажды грезил сборкой такого большого порядка, и практиковался на виртуальном кубике в компьютерной программе-симуляторе. Тогда это заняло около 1 часа 20 минут, что дает возможность прикинуть время для реальной сборки.
И вот я решился заскрамблить этого исполина! Предполагая, что сборка затянется более часа, надо предварительно к ней подготовиться. Это хоть и звучит забавно, но ничего смешного в этом я не видел. Вначале я постриг ногти и срезал заусеницы (поверьте, это еще как мешает), сходил в туалет (без комментариев; собирать желательно без перерыва), умылся и протер глаза (ведь напряжение для зрительных нервов предстояло еще то), слегка размял кисти рук (вертеть же в руках почти килограммовый пазл), удобно уселся в кресле – и понеслось…
Что уж говорить о сборке, если даже скрамблить такую громадину составляет труда. Две минуты мешал, пока не посчитал этого достаточным, чтобы как можно меньше оставалось рядом смежных цветов. Заблаговременно составил табличку, в которую записывал промежуточные результаты сборки отдельных этапов. Для меня было крайне любопытно: сколько времени займет решение каждого из этапов и подэтапов сборки. Итак, ниже я привожу эти самые результаты:
| # | Этап сборки: | Время сборки: | % от общего времени: |
| скрамбл | 2 мин | ||
| 1. | первая сторона | 16 мин 56 сек | 20.5% |
| 2. | противоположная сторона | 8 мин 56 сек | 10.8% |
| 3. | третья сторона | 10 мин 54 сек | 13.2% |
| 4. | четвертая сторона | 11 мин 59 сек | 14.5% |
| 5. | пара последних сторон | 9 мин 1 сек | 10.9% |
| 6. | первые четыре ребра | 8 мин 50 сек | 10.7% |
| 7. | следующие четыре ребра | 5 мин 10 сек | 6.3% |
| 8. | последние четыре ребра с паритетом | 9 мин 1 сек | 10.9% |
| 9. | этап 3x3x3 | 1 мин 44 сек | 2.1% |
| Итого: | 1 час 22 минуты 31 секунда | 100% |
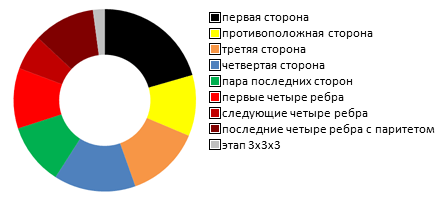
Примерно так я и предполагал: полтора часа выделил свободного времени – в них и уложился! Удивительно, что время сборки реальной головоломки почти совпало со временем её же виртуального представления. К слову сказать, на днях на YouTub`е появилось видео одного парня и его сборки 11x11x11 http://www.youtube.com/watch?v=W5vOBMzspww – он справился за 1 час 13 минут. Оказывается разброс результатов по времени не так уж и велик. И я чувствую в себе силы собирать за 1 час где-то после пятой сборки этой громадины!..
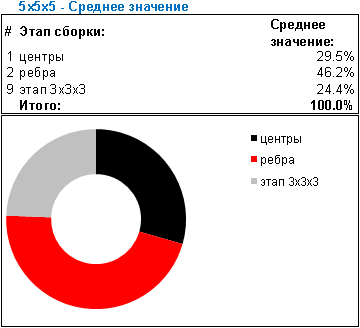
Теперь хочу немного акцентировать внимание на таблице выше, и проанализировать результаты. Естественно, по одной лишь сборке мало о чем приходится говорить, ведь сверять пока не с чем.
Первую грань я с непривычки складывал очень долго, хотя на этом этапе как раз есть где разгуляться, и свобода перемещений никакими собранными блоками не ограничивается. Затянутость первого этапа можно подтвердить хотя бы тем, что второй этап я сложил уже вдвое быстрее, не смотря на то, что нужно следить за неразбиением сложенной первой грани. Думаю, что при следующих сборках такая ошибка уже не повторится. Компоновка третей и четвертой сторон еще более стеснены с своих маневрах. Пара последних сторон складывается вместе сложнее, чем это, к примеру, делается на 7x7x7, – но зато куда увлекательнее. На все грани ушло 57 минут 46 секунд, что составляет почти 70% от общего времени решения кубика 11x11x11. Потрясающе, правда?! И чем большего порядка будет куб – тем дольше складывать центры.
Переключиться на решение ребер сложно, после часа, проведенного за складыванием центров. Визуально надо концентрироваться на узеньких полосках, к тому же стикеры отливают отраженным светом. К моему удивлению, ребра складывались быстрее, чем я предполагал. Следует как можно больше избегать лишних “переворотов” ребер (flip), с помощью известного алгоритма, так как он неуклюже получается на таком большом кубе. Лучше всего один раз скомпоновать все элементы ребра повернутые в одну и в другую стороны – а потом единожды применить flip-алгоритм. Решение паритета – самая ожидаемая мною вещь. Завораживающее занятие, когда остаются только два нерешенных ребра! В моём случае он попался не очень тяжелым, чему я немного расстроился, – или же он в принципе не так уж сложен… На всё про всё ушло 23 минуты 1 секунда, что составляет 28% от общего времени сборки.
Последний этап, сродни классическому 3x3x3, очень забавно проделывать на таком большом кубе. Руки так и чешутся применять фингертиксы (fingertics) – но 900-граммовая, плывущая по слоям и скользящая в руках махина диктует свои правила. 1 минута 44 секунды – таков финишный порыв, не многим более 2% от общего времени кропотливой сборки 11x11x11.
В течении этих полутора часов я непрерывно обливался пОтом, не смотря на то, что сидел лишь в майке с февралем за окном. Такова концентрация и борьба с выравниванием слоев. Дабы не допускать проскальзывания, и не перегружать кисти рук – я клал этот, почти что килограммовый, агрегат себе на пузо. Оно-то смешно, но парень на видео складывающий “одинадцатку” (по ссылке где-то указанной выше), делал то же самое – и я его прекрасно понимаю. Сам кубик по ощущениям немного разболтался, благодаря чему начал лучше резать углы, хотя вначале это трудно было делать. Глаза после окончания сборки болели, и уже хотелось спать, на часах полпервого ночи… Но эмоций валом! Неописуемый подарок себе увидеть вновь собранным этого гиганта после долгих потуг. Мерно переливающиеся стикеры, при свете полуночной лампы, – идиллия и торжество гения, тихо радующегося решению самой сложной головоломки.
Понравилось жутко! Надо будет как-то еще разок повторить… ;)
Глава 5. Напутствие к сборкам 11x11x11.
В след за первой экспериментальной сборкой, через неделю, на следующих выходных, – я повторил этот подвиг. На сей раз для истории я запечатлел это действие на видео. Результат второй сборки уже был куда приемлемее: 1 час 6 минут 29.64 секунды. Чувствовалась уверенность в силах, первый опыт принес свои плоды: уже не повторял прежние ошибки, идя ложным путем, а сразу выстраивал нужные блоки сложенных элементов там где и когда это нужно.
click to open video
Видео: 11x11x11 Cube Solving (1h:6m:29s.64ss)
В действительности трудно себя заставить сесть за сборку такого монстра. Для этого, как говорится, нужно “быть в форме”. Но даже с ней потратить один час времени с усердием и полной концентрацией – изматывающее испытание. Хотя, и не менее от того желанное. В промежутках между уикендами, когда я могу себе позволить выделить время на такое развлечение, кубик тоже не простаивает. Кроме серьезного занятия – сборки, есть разрядка попроще – узоры на кубике (patterns). Грех не воспользоваться возможностью такого широкого “холста” для пиксельного арта. Множество известных узоров более мелких кубиков прекрасно аппроксимируются на размер 11x11x11 – и получаются изумительные рисунки. Даже то, что для меня ранее удивительным смотрелось на кубе 7x7x7 – теперь и рядом не стоит на просторах, открывающихся с поистине большим кубом. Единственное, что делать такие узоры намного дольше, и коль ошибешься – придется долго и долго исправлять свою ошибку…



click to zoom to actual resolution
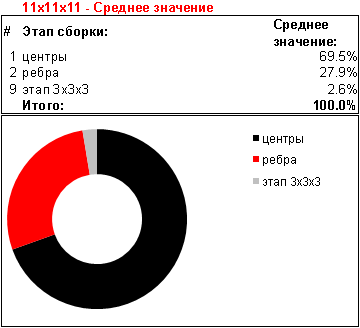
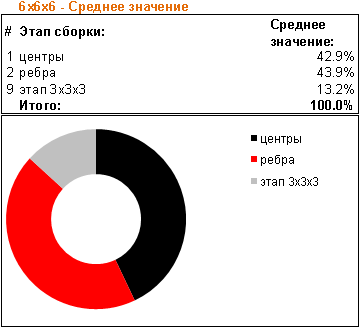
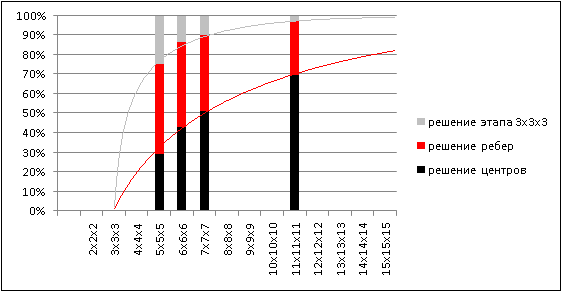
На момент написания статьи я собрал 11x11x11 на время всего трижды. Последняя попытка дала приятные результаты, когда по времени я вышел из часа: 58 минут 50.49 секунды. Эти три сборки с детализированными результатами уже могут составить примерную картину затрачиваемых усилий на каждом из этапов. На основании этих данных можно делать некоторые интересные выводы. Если, вдобавок к результатам по 11x11x11, проделать подобные расчеты и для кубов других порядков – то можно исследовать тенденцию в зависимости от размера, а также предсказывать сборку кубов любого порядка. Этим я и занялся. Ниже привожу сравнительные таблицы затраченного времени сборки, как в абсолютных, так и в относительных величинах.
Одиночной попытки решения 11x11x11 было бы мало для статистики. Отклонения на различных этапах достаточно ощутимы – так что по завершению трех попыток уже можно примерно судить о результатах. Аналогичные измерения я провел и для куба 7x7x7. Так как его складывать “быстрее” – то я сделал пять попыток. дабы проследить тенденцию и на других порядках – также провел вычисления и для более “мелких” кубов.
Измерения нельзя назвать абсолютно объективными и всеобъемлющими, но всё же претендующими на близость к истине. Оценивались результаты только моих сборок, то есть лишь одного участника с определенными навыками. Однако я отмечу, что за основу брались относительные величины – процент от общего времени сборки, а не абсолютные – конкретное время в минутах. К тому же, я расцениваю свои умения в сборке кубов различных порядков примерно одинаковыми. Следует также отметить, что результирующая кривая оценки времени сборки не применима к размерам 3x3x3 и 2x2x2 – так как там используются базовые методики, которые для больших кубов являются лишь отдельными этапами. Для кубов четных порядков также есть нюансы – там присутствуют этапы решения дополнительных паритетов.
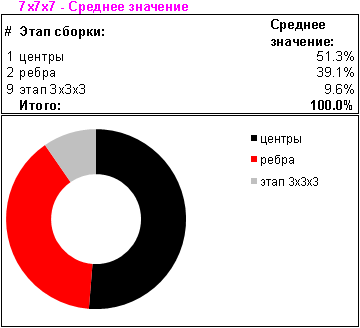
Теперь расскажу о приобретенном опыте самой сборки пазла. Из-за физической проблемы выравнивания слоев – предпочтительно использовать методы и алгоритмы, требующие наименьших “переворотов”, и переходов на повороты перпендикулярных слоев. Чаще надо вертеть внешние грани, нежели внутренние слои. Это удобнее еще и с той точки зрения, что ладонью легче повернуть внешний ярус, нежели обхватывать совсем не маленький куб для операций с внутренними ярусами.
На этапах сборки центров – эффективнее собирать их “столбиками”, что существенно снижает общее время по сравнению со сборкой “улиткой”. Это легко продемонстрировать для размера 11x11x11. Собирая “столбиками” – их надо всего 9 штук, чтобы скомпоновать однотонный центр. При сборке же “улиткой” – потребуется 16 раз загонять собранные блоки. Это в случае куба 7x7x7 не шибко принципиален метод для центров – но для больших размеров разница очевидна и на лицо.
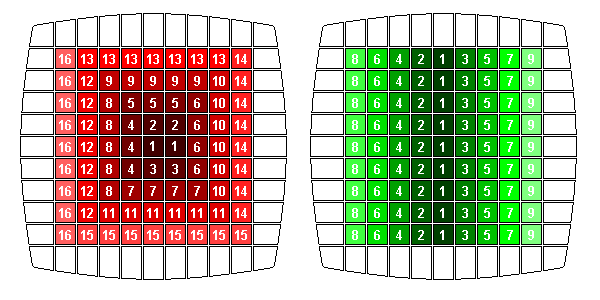
По поводу спаривания ребер я уже писал: что лучше за раз скомпоновать и применить flip-алгоритм, для экономии времени. После спаривания очередного ребра желательно не возвращать центры в их исходное сложенное состояние, но продолжать искать части для следующего. Восстановление центров занимает достаточно времени, и не окупает применение более простых flip-алгоритмов. Оно-то конечно больше сбивает с толку, когда не видишь сложенного центра, и уповаешь на то, что не сделал никаких ошибок на предыдущих переворотах ребер. Однако здорово экономит время и лишние движения.
Когда добираешься до этапа паритета двух последних ребер – следует не спешить и внимательно продумать его решение. Лучше всего, для начала, сделать пару простеньких паритетов для приведения внешних частей в удобное состояние. А потом одним громоздким алгоритмом, с захватом всех необходимых слоев, решить остающийся паритет. И даже после этого, наверняка, придется переворачивать пары на последнем ребре. В любом случае, весь этот этап машинальный и не требует особой сообразительности – всё построено на конкретных алгоритмах.
Глава 6. Головоломка в головоломке.
Каждого мальчишку в душе распирает любопытство заглянуть во внутрь своей игрушки, коль бы сложной она ни была, еще до того как он ею наиграется. Конечно же, в связи с этим встают две проблемы: как бы её так разобрать, чтобы не сломать; а после собрать обратно, без “лишних” деталей? Скажите, если я не прав! Ну вот согласитесь: чем не головоломка?
Признаюсь честно: еще когда я грезил заполучением куба 11x11x11 – мне было интереснее его “разобрать” как механизм, нежели “сложить” как пазл. Поскольку в навыках второго я был уверен, – а вот осведомленности первого – не совсем. И чтобы старания не пропали даром, я решил процесс задокументировать на фото: все тонкости строения единого механизма из шестисот отдельных деталей. Своеобразную фотосессию эротического содержания: обнажающегося 11x11x11, я представляю вам в этой главе ниже.



click to zoom to actual resolution
Первым делом я залез под самые легкодоступные компоненты: крышечки центральных элементов. Под ними показались шапки крепящих винтов. Не берусь утверждать, что это именно винты, а не заклепки, – поскольку несколько оборотов отверткой не дали ощутимого эффекта ослабления натяжения. Далее следовало как-то подобраться к кубу с самой его уязвимой точки, с которой потихоньку начать вынимать составные элементы один за другим. Как я уже оговаривал ранее: наименее глубоко залегаемая деталь находится на том самом месте, что и в кубике 7x7x7, – с неё я и начал.



click to zoom to actual resolution
После выемки пары десятков кусочков – дальше куб начинает уже распадаться самостоятельно. Поэтому вынимал я их аккуратно, попутно запечатлевая на фото все нюансы открывающего механизма. Разбирать следует не спеша, по “четвертям” – то есть блоками, как бы облепляющими вокруг, каждый из восьми углов. Ведь сам по себе “уголок” имеет массивное основание в виде срезанной части сферы.
По мере продвижения вглубь, я вынимал составные кусочки всё большего размера. Но даже самые маленькие были изготовлены с продуманной точностью и скрупулезностью: не было видно заусениц, царапин, стенки внутренних полостей ни за что не цеплялись при проворачивании, никакого лишнего материала – для облегчения совокупного веса головоломки. Однако, ожидаемо огорчило спаивание больших составных частей, литых половинками: на месте склеивания щель зияла, порой, в полмиллиметра толщиной. Хотя это совершенно не мешало работе аппарата. Всё это соприкасалось без какой бы то ни было заводской смазки. Добравшись до сердцевины, когда уже вынут громоздкий угловой элемент, я увидел на нем легкое поблескивание и малую отдушину то ли смазки, то ли конденсата, – в общем, осталось загадкой.



click to zoom to actual resolution
По конструкции 11x11x11 имеет среди всех своих шести сотен составляющих элементов, как это ни удивительно, всего 27 уникальных, из которых 6 пар симметричных между собой по виду. А также внутренняя крестовина и шесть винтов с пружинами. Эта простота объясняется множеством степеней свободы (читай: симметрий) такой стереометрической фигуры, как куб. Большинство элементов продублированы по 24 штуки. И вся хитрость механизма состоит в том, чтобы все кусочки расформировать на 24 группы, и состыковать во всевозможных симметриях и ориентациях. Тогда, в итоге, получаем 24 блока, держащихся на каркасе крестовины.



click to zoom to actual resolution
Накануне разборки 11x11x11 – я разбирал кубик 7x7x7. Во-первых, чтобы оценить и сравнить общество количество составляющих элементов, что называется, в натуре. А во-вторых, дабы попрактиковаться с разборкой/сборкой, и без сюрпризов скомпоновать его обратно. Иначе, было бы печально смотреть на груду деталей, некогда именовавшуюся кубом, не зная с чего начать восстановление. Как я упоминал ранее: у 11x11x11 – 602 разборных элемента. И ,как известно: у 7x7x7 – их 218. Ну, то есть, где-то в три раза больше! “Семерку” я разобрал полностью, и выложил все составляющие на столе. “Одинадцатку” же я решил не терзать, и разобрал ее только наполовину. Коль бы всю – то стало бы рутиной на полдня собирать обратно; все детали там такие же, ничего нового я бы не увидел; да, к тому же, не хватило бы столешницы разложить все элементы. Привожу фотографии разложенных по кусочкам двух кубов для сравнения: 11x11x11 и 7x7x7 (не забывайте, что “исполин” разобран лишь наполовину). Картина завораживающая!
11x11x11



click to zoom to actual resolution
7x7x7



click to zoom to actual resolution
Теперь моё любопытство удовлетворено, считаю, как и ваше. Куб я сложил обратно без приключений и “лишних” деталей. Забавно было видеть на столе сумбурную кучу белого пластика со сверкающими, разноцветными наклейками – а после их сортировать, раскладывать по группам симметрий, и в параллельные ряды на столе – ради эффектного фотоснимка. Еще одна головоломка изучена вдоль и поперек, раскрыты все секреты. Теперь моя коллекция пополнилась незаурядным образцом!
Помнится, как однажды на форуме по обсуждению головоломок кто-то сказал, что: безумно тратить такие большие деньги на покупку 11x11x11 или подобных, коль всё равно соберете этот пазл раз десять от силы за всё время, и поставите за стекло любоваться, да друзьям показывать… Но ведь в этом-то и смысл! Особо грандиозных надежд полагать и не стоит, приобретая такие вещи. Их привлекательность как раз и состоит в уникальности экспоната для коллекции. Уж тем более, когда вы прилагали недюжинные усилия в осуществлении желания, и гонялись за ним, дабы заполучить правдами и неправдами… Когда вначале пути ты и мечтать не мог держать его в руках, – а в итоге чувствуешь, что своим упорством и настойчивостью ты заслужил!..
В конце концов, кроме дивного экземпляра на полочке за стеклом, как собственного утешения, – я имел возможность поведать вам об этом уникальном кубике во всех подробностях. Многое осталось недосказанным, части бы уделить больше внимания, – но и без того обзор получился куда более развернутым и во многих аспектах. Окроме как собирать головоломки, мне также приятно нести мысль в массы, приобщать к интеллектуальной культуре, зажигать огонек любознательности. Дерзайте!
Алексей Гуров
—
(c) Просьба, если уж и копировать материал статьи, – то с обязательной ссылкой на этот источник и автора. Спасибо.







напиши конкрентно где куить и почем